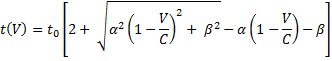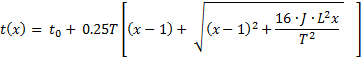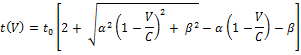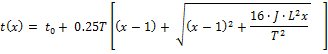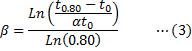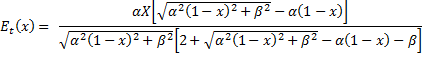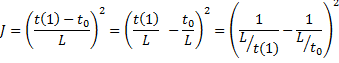|
||||||||||||||||||||||||||||||||
Introducción
En cualquier sistema de transporte, el tiempo de viaje es un elemento central para evaluar el desempeño del sistema, y suele ser un elemento de decisión para los usuarios del servicio. En el transporte cotidiano por automotor ya sea en automóvil, autobús o camión tanto en áreas urbanas como en carreteras, se percibe claramente cómo a medida que hay más vehículos compartiendo el camino, el tiempo de viaje para llegar al destino aumenta. Esta situación es la experiencia de la congestión vehicular que conlleva impactos no deseados, como son: un mayor gasto de combustible, el retraso en las actividades de los viajeros o en la entrega de mercancías, el incremento de la contaminación del aire, etc. En la planeación de los sistemas de transporte, tener una representación razonable de cómo la congestión vehicular incrementa el tiempo de viaje en las distintas rutas de la red de transporte es fundamental para identificar medidas atenuantes, acciones correctivas o propuestas de mejoras a la infraestructura, a los sistemas de control de tráfico y a las políticas de uso de la red por las distintas clases de usuarios. En este trabajo se examinan los modelos matemáticos más utilizados en la planeación del transporte para representar la dependencia del tiempo de viaje en función de los volúmenes vehiculares que ocupan las vías, en el caso del autotransporte. Estos modelos se conocen en la literatura como funciones volumen-demora, ya que relacionan la demora en el tiempo de viaje con los volúmenes vehiculares que circulan en las vías. El objetivo principal es la revisión de estos modelos y el uso reportado en la literatura; el examen de sus funciones con sus respectivos parámetros y el análisis de su aplicabilidad en el contexto de la planeación del transporte en México.
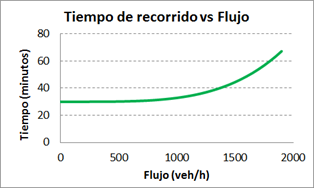
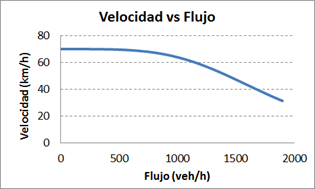
El diagrama fundamental: velocidad vs flujo vehicular El efecto más directo de la congestión que se percibe en una red de transporte es la reducción de la velocidad y el aumento resultante en el tiempo de viaje para llegar al destino. Los ingenieros de tráfico han examinado esta situación determinando las relaciones que se dan entre las variables que explican el fenómeno: la velocidad (km/h), la densidad vehicular (veh/km) y el flujo vehicular (veh/h). El esquema básico que muestra estas relaciones es llamado el Diagrama Fundamental, y una de sus representaciones más comunes son las curvas de flujo-velocidad, que muestran cómo la velocidad de recorrido en un tramo es afectada por el flujo vehicular presente. La Figura 1 ilustra una curva típica de flujo-velocidad y su correspondiente curva de flujo-tiempo de viaje donde se supone un tramo de 35 km con una velocidad de flujo libre de 70 km/h y una capacidad máxima de 1800 veh/h.
Figura 1. Ejemplo de curvas de flujo-velocidad y de flujo-tiempo (elaboración propia). Las curvas de la Figura 1 ilustran la experiencia común de transitar por una vía a la cual se van incorporando más y más vehículos. Si el flujo es cero, un solo vehículo puede recorrerlo en promedio a 70 km/h; es la llamada velocidad de flujo libre, la velocidad media de un vehículo que avanza sin obstáculos considerando las características y la capacidad máxima del camino (expresada en vehículos por hora). A esta velocidad, el recorrido dura 30 minutos. Cuando el flujo llega a al máximo de 1800 veh/h, la velocidad baja a 30 km/h y el tiempo de recorrido aumenta a 60 minutos. Con flujos menores a 750 veh/h, los cambios de velocidad y de tiempo de recorrido varían muy poco; pero con flujos mayores los cambios son más notorios debido a la congestión vehicular. La forma de la curvas en la Figura 1 depende de la formulación matemática que relaciona el flujo con la velocidad y con el tiempo de recorrido. De estas relaciones, la que hay entre flujo y tiempo es de interés práctico por el impacto que los retrasos tienen en los viajes por motivo de trabajo, escuela, servicios de salud, etc. o en el movimiento de carga, que lleva a mayores costos operativos. La expresión formal de estas relaciones son las funciones volumen-demora que modelan la dependencia del tiempo de viaje del volumen vehicular en el camino. Varias formulaciones para estas funciones están en la literatura de transporte y en reportes de profesionales de la planeación del transporte que las usan. De las más conocidas son: la función BPR, la función cónica y la de Akcelik, que se comentan en las siguientes secciones. Funciones de volumen-demora Una Función
Volumen-Demora (FVD) 1.
El
argumento 2.
3.
Conviene
que 4.
Como
el tiempo de viaje generalmente aumenta sin brusquedad, conviene que Algunas funciones propuestas con estos rasgos son: · La función de Smock (1962) propuesta para el Detroit Metropolitan Area Traffic Study, (1953 – 1955) en los Estados Unidos, precursor de la metodología de planeación de las cuatro etapas para el transporte:
Donde
·
La
función de Overgaard (1967) que generaliza la de Smock al cambiar la función
exponencial de base
· La función del Bureau of Public Roads (BPR) norteamericano (1962), ampliamente usada en ejercicios de planeación del transporte:
donde
· La función Cónica de volumen-demora:
donde
· La función de Akcelik:
donde
De estas funciones solamente la de Smock tiene una fórmula única que depende del volumen vehicular circulante; las demás funciones propuestas tienen parámetros en sus definiciones que es preciso calibrar para una representación adecuada de los tiempos de viaje en los tramos. La Figura 2 ilustra
la función de Smock y la BPR con dos conjuntos de parámetros para el tramo
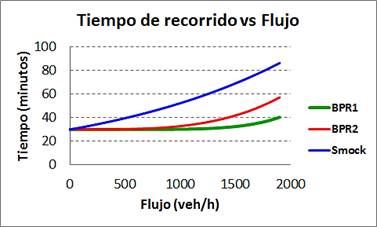
supuesto anteriormente, donde La BPR1 es para a = 0.25 y b = 6, mientras que la BPR2 es con a = 0.75 y b = 3.5. Como muestra la Figura 2, la función de Smock pronostica un poco más de 80 minutos en el flujo de saturación; la función BPR1 indica cerca de 40 minutos y la BPR2 poco menos de 60 minutos. Surge entonces la cuestión de elegir la función que más se asemeje al comportamiento real de los tiempos de viaje, lo que lleva al problema de calibración de las funciones que se comenta más adelante.
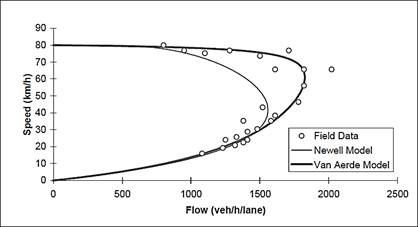
Figura 2. Curvas de volumen-demora para la función de Smock y para BPR. (elaboración propia). La Figura 2 también muestra que la función de Smock aumenta el tiempo de viaje de modo constante desde de cero, mientras que las funciones BPR aumentan el tiempo muy poco para flujos menores de 1000 veh/h. Este último rasgo de las BPR es útil para representar niveles de servicio en el tramo, al aumentar el flujo. La calibración de las funciones de volumen-demora (FVD) Una buena representación de una función volumen-demora requiere en principio recopilar datos de campo de los flujos reales observados en el tramo de interés. Un dato fácilmente observable en un tramo es la velocidad de circulación para distintos volúmenes vehiculares. Colectando estos datos, se obtiene una curva de flujo-velocidad como la de la Figura 3, donde los puntos son mediciones de velocidad para distintos niveles de flujo, y las curvas mostradas son modelos de ajuste para la relación flujo-velocidad. La curva flujo-velocidad muestra el comportamiento típico del flujo en una vialidad, partiendo de la velocidad de flujo libre (80 km/h en el ejemplo) y se mantiene más o menos constante hasta que el flujo llega a la saturación (unos 2000 veh/h) donde la velocidad se reduce (cerca de 60 km/h). Esta parte de la curva representa los niveles de servicio desde “A” en condiciones de flujo libre hasta el “E” en el que la congestión ya es manifiesta (Papacostas, 1987). Los puntos en la parte baja de la curva tienen valores de velocidad menores que la velocidad a saturación, aunque ocurren para flujos menores; esto corresponde al comportamiento caótico del tráfico cuando flujo adicional intenta entrar al tramo saturado y surgen colas que entorpecen más la circulación. Esta parte de la curva representa el nivel de servicio “F” en el cual el flujo vehicular es muy forzado y las colas avanzan en oleadas con comportamiento inestable.
Figura 3. Ejemplo de curva típica de flujo-velocidad (Rakha, H., 2009) Ya con mediciones de flujo-velocidad, se aplican procedimientos de ajuste de curvas para generar una función matemática cuya gráfica se acerque lo mejor posible a los puntos observados. Es común ajustar con la técnica de mínimos cuadrados, proponiendo una fórmula para la curva teórica y estimando los parámetros que describen esa curva particular que se aproxima a los puntos. Con la función matemática flujo-velocidad, más la longitud del tramo, se construye la función de volumen-demora para el tiempo de viaje en función del flujo circulante. El proceso descrito requiere colecta de datos en campo, lo cual implica gastos monetarios, personal capacitado, organización de equipos y tiempo, recursos que generalmente son limitados y difíciles de conseguir. Este artículo propone un esquema alterno a la colecta masiva de datos para estimar parámetros de las funciones volumen-demora. Se basa en el análisis matemático de las funciones y la interpretación de sus parámetros. Para comenzar, se observa el comportamiento de las funciones volumen-demora (FVD) en los extremos de sus dominios de definición, como se muestra en la Tabla 1. Tabla 1. Comportamiento de las FVD en sus valores mínimo y máximo (elaboración propia)
La Tabla 1 muestra
que las FVD calculan correctamente el tiempo · La función de Smock da un aumento del tiempo por un factor de 2.7 aproximadamente para el flujo de saturación. ·
Con
la función de Overgaard el factor de aumento del tiempo de viaje es ·
Con
la función BPR el factor de aumento es · Con la función Cónica el factor de aumento es 2; esto corresponde a una regla práctica en estudios de tráfico, que supone que en saturación, el tiempo de recorrido aproximadamente se duplica. ·
Con
la función de Akcelik, el aumento del tiempo de viaje no aparece como factor,
sino como un sumando igual a Las estimaciones de los aumentos del tiempo de viaje para la saturación en las FVD mostradas, salvo la de Smock y la Cónica, dependen de los parámetros de sus formulaciones matemáticas. La interpretación matemática de los parámetros de las FVD puede aclarar su significado en la formulación y sugerir formas alternas de estimar estos parámetros, como se describe enseguida.
Intepretación de parámetros 1) La función de Overgaard. Esta función puede reescribirse como:
donde
Puede verse 2) La función BPR. Reescribiendo la BPR,
con la variable
En el valor de la
función en saturación,
Así,
Con lo que La interpretación de
De donde se obtiene:
Así,
3) La función Cónica. Esta función
también puede redefinirse en términos del porcentaje de flujo
De la Tabla 1 se ve
que la función cónica siempre asigna el doble del tiempo de flujo libre al
nivel de flujo de saturación, en la ecuación (4) resulta: Para dar una interpretación
de
Por lo que la elasticidad de la función cónica en la ecuación (4) resulta:
Evaluando esta elasticidad en los puntos máximo y mínimo de saturación de flujo:
Por lo que 4) La función de Akcelik. En esta función, el
único parámetro es De la Tabla 1 se
observa que cuando se tiene el nivel de saturación
Resolviendo la
ecuación anterior respecto de
La última expresión de las ecuaciones previas significa que:
Por lo que En un desarrollo
similar, Ortúzar y Willumsen (2011) sugieren que el parámetro
Donde
Conclusiones Las funciones de volumen-demora son un elemento básico del proceso de modelación del tráfico y de su consecuente aplicación a la planeación de redes de transporte terrestre. La relevancia de tener funciones volumen-demora que repliquen razonablemente los tiempos de recorrido en presencia de congestión se basa en que las decisiones de los automovilistas, camiones de carga, autobuses y otros usuarios de una red vial suelen estar influidas por los tiempos estimados de recorrido de las rutas que eligen. Los procedimientos tradicionales de colectar datos de campo para construir relaciones flujo-velocidad, para luego estimar funciones volumen-demora, es sin duda deseable y puede dar buenos resultados, pero enfrenta el problema común de la escasez de los recursos necesarios para llevar a cabo las mediciones de modo adecuado. El análisis matemático del comportamiento de las funciones volumen-demora más comúnmente usadas en los ejercicios de planeación del transporte puede ser un camino alterno a la colecta masiva de datos de flujo-velocidad en las redes viales. La interpretación de los parámetros de las funciones ya comentadas sugiere hacer mediciones algo más sencillas y de menores costos para estimar estos parámetros. De las observaciones
sobre los parámetros para
·
Mediciones
de aumentos porcentuales del tiempo de flujo libre para estimar el parámetro ·
Estimar
la elasticidad del tiempo de recorrido respecto del flujo, es decir la
elasticidad demora-volumen en el punto de saturación a fin de estimar el
parámetro ·
Estimar
los tiempos y/o las velocidades en el nivel de saturación para estimar el
parámetro Estas interpretaciones permiten hacer estimaciones de los parámetros de interés con un número de observaciones más reducido que el que se requiere en estudios típicos de flujo-velocidad, lo que agiliza el proceso de calibración. Este enfoque de hacer un análisis matemático del comportamiento de las funciones en sus respectivos dominios, así como de las posibles interpretaciones de sus parámetros puede en principio extenderse a otras formulaciones de FVDs y aclarar ideas del significado operativo que tienen las formulaciones y de la calidad de su representación del tiempo de viaje en las vialidades.
Bilbiografía Caliper Corporation. (2005). Travel Demand Modeling with TransCAD 4.8. Caliper Corporation. USA. Moreno, E., Rico, O. y Bustos A. (2014). Funciones volumen-demora en la modelación de flujos vehiculares. Publicación Técnica No. 427. Instituto Mexicano del Transporte. Sanfandila, Querétaro, México. Ortúzar. J.D., Willumsen, L.G. (2011). MODELLING TRANSPORT. 4th Edition. John WIley & Sons. Chichester, UK Papacostas, C.S. (1987). Fundamentals of Transportation Engineering. Prentice-Hall Inc. USA. Rakha, H. (2009). Validation of Van Aerde’s simplified steady-state car-following and traffic stream model. Transportation Letters: The International Journal of Transportation Research (2009) 1: (227-244) Speiss, H. (1990). Conical Volume-Delay Functions. Transportation Science. Vol. 24, No. 2. ORSA, Baltimore, USA. TRB. Transportation Research Board. (2000). Highway Capacity Manual 2000. National Research Council. Washington, D.C.
MORENO Eric |